Berkeley admission data
- Study carried out by the Graduate Division of the University of California, Berkeley in the early 70’s to evaluate whether there was a gender bias in graduate admissions.
- The data come from six departments. For confidentiality we'll call them A-F.
- We have information on whether the applicant was male or female and whether they were admitted or rejected.
- First, we will evaluate whether the percentage of males admitted is indeed higher than females, overall. Next, we will calculate the same percentage for each department.
3 / 26
Data
## # A tibble: 4,526 × 3## admit gender dept ## <fct> <fct> <ord>## 1 Admitted Male A ## 2 Admitted Male A ## 3 Admitted Male A ## 4 Admitted Male A ## 5 Admitted Male A ## 6 Admitted Male A ## 7 Admitted Male A ## 8 Admitted Male A ## 9 Admitted Male A ## 10 Admitted Male A ## 11 Admitted Male A ## 12 Admitted Male A ## 13 Admitted Male A ## 14 Admitted Male A ## 15 Admitted Male A ## # … with 4,511 more rows## # A tibble: 2 × 2## gender n## <fct> <int>## 1 Female 1835## 2 Male 2691## # A tibble: 6 × 2## dept n## <ord> <int>## 1 A 933## 2 B 585## 3 C 918## 4 D 792## 5 E 584## 6 F 714## # A tibble: 2 × 2## admit n## <fct> <int>## 1 Rejected 2771## 2 Admitted 17554 / 26
What can you say about the overall gender distribution? Hint: Calculate the following probabilities: P(Admit|Male) and P(Admit|Female).
ucbadmit %>% count(gender, admit)## # A tibble: 4 × 3## gender admit n## <fct> <fct> <int>## 1 Female Rejected 1278## 2 Female Admitted 557## 3 Male Rejected 1493## 4 Male Admitted 11985 / 26
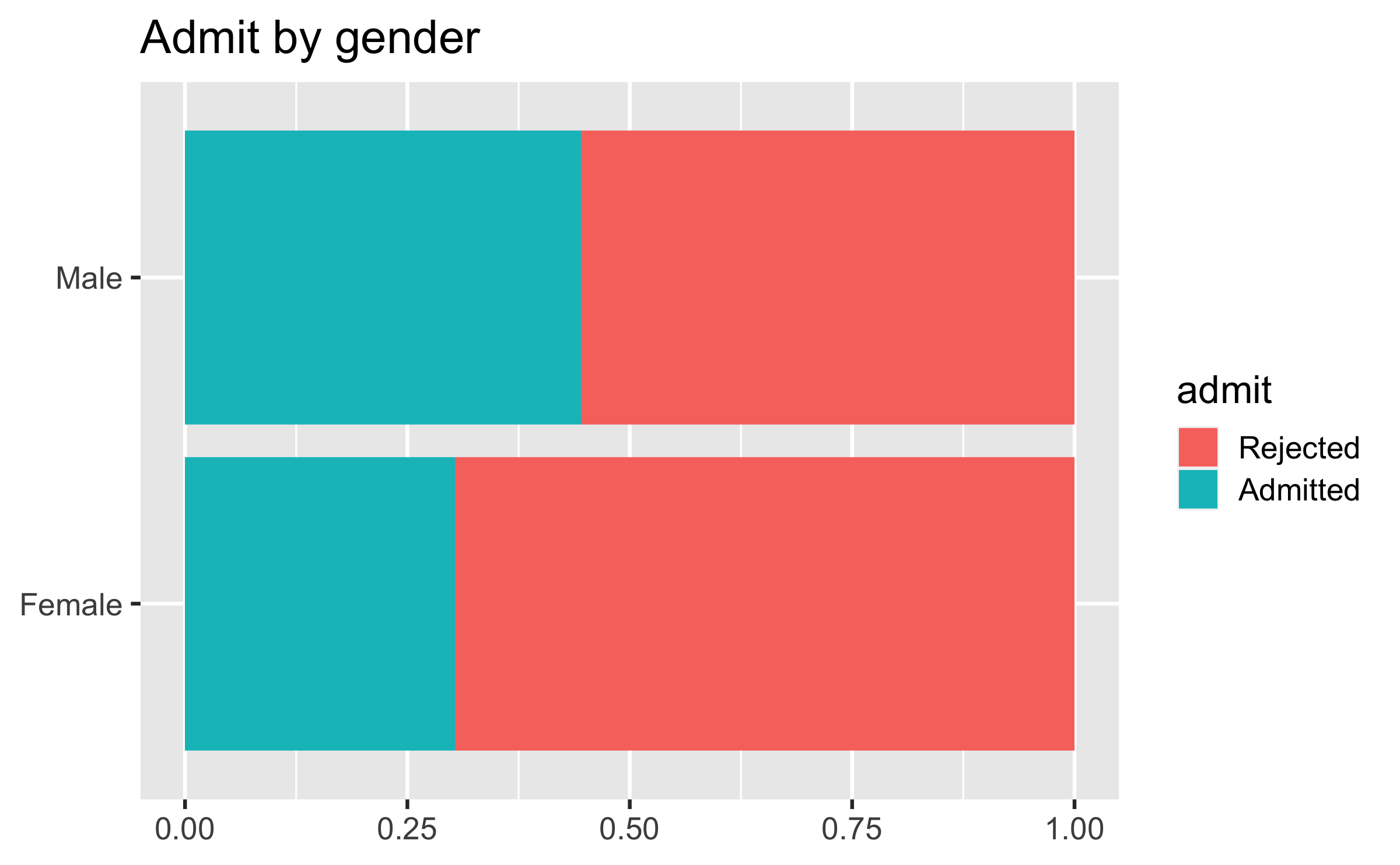
ucbadmit %>% count(gender, admit) %>% group_by(gender) %>% mutate(prop_admit = n / sum(n))## # A tibble: 4 × 4## # Groups: gender [2]## gender admit n prop_admit## <fct> <fct> <int> <dbl>## 1 Female Rejected 1278 0.696## 2 Female Admitted 557 0.304## 3 Male Rejected 1493 0.555## 4 Male Admitted 1198 0.445- P(Admit|Female) = 0.304
- P(Admit|Male) = 0.445
6 / 26
Overall gender distribution

ggplot(ucbadmit, aes(y = gender, fill = admit)) + geom_bar(position = "fill") + labs(title = "Admit by gender", y = NULL, x = NULL)7 / 26
What can you say about the gender distribution by department ?
ucbadmit %>% count(dept, gender, admit)## # A tibble: 24 × 4## dept gender admit n## <ord> <fct> <fct> <int>## 1 A Female Rejected 19## 2 A Female Admitted 89## 3 A Male Rejected 313## 4 A Male Admitted 512## 5 B Female Rejected 8## 6 B Female Admitted 17## # … with 18 more rows8 / 26
Let's try again... What can you say about the gender distribution by department?
ucbadmit %>% count(dept, gender, admit) %>% pivot_wider(names_from = dept, values_from = n)## # A tibble: 4 × 8## gender admit A B C D E F## <fct> <fct> <int> <int> <int> <int> <int> <int>## 1 Female Rejected 19 8 391 244 299 317## 2 Female Admitted 89 17 202 131 94 24## 3 Male Rejected 313 207 205 279 138 351## 4 Male Admitted 512 353 120 138 53 229 / 26
Gender distribution, by department

ggplot(ucbadmit, aes(y = gender, fill = admit)) + geom_bar(position = "fill") + facet_wrap(. ~ dept) + scale_x_continuous(labels = label_percent()) + labs(title = "Admissions by gender and department", x = NULL, y = NULL, fill = NULL) + theme(legend.position = "bottom")10 / 26
Closer look at departments
## # A tibble: 12 × 5## # Groups: dept, gender [12]## dept gender n_admitted n_applied prop_admit## <ord> <fct> <int> <int> <dbl>## 1 A Female 89 108 0.824 ## 2 A Male 512 825 0.621 ## 3 B Female 17 25 0.68 ## 4 B Male 353 560 0.630 ## 5 C Female 202 593 0.341 ## 6 C Male 120 325 0.369 ## 7 D Female 131 375 0.349 ## 8 D Male 138 417 0.331 ## 9 E Female 94 393 0.239 ## 10 E Male 53 191 0.277 ## 11 F Female 24 341 0.0704## 12 F Male 22 373 0.0590ucbadmit %>% count(dept, gender, admit) %>% group_by(dept, gender) %>% mutate( n_applied = sum(n), prop_admit = n / n_applied ) %>% filter(admit == "Admitted") %>% rename(n_admitted = n) %>% select(-admit) %>% print(n = 12)12 / 26
Relationship between two variables
## # A tibble: 8 × 3## x y z ## <dbl> <dbl> <chr>## 1 2 4 A ## 2 3 3 A ## 3 4 2 A ## 4 5 1 A ## 5 6 11 B ## 6 7 10 B ## # … with 2 more rows
14 / 26
Relationship between two variables
## # A tibble: 8 × 3## x y z ## <dbl> <dbl> <chr>## 1 2 4 A ## 2 3 3 A ## 3 4 2 A ## 4 5 1 A ## 5 6 11 B ## 6 7 10 B ## # … with 2 more rows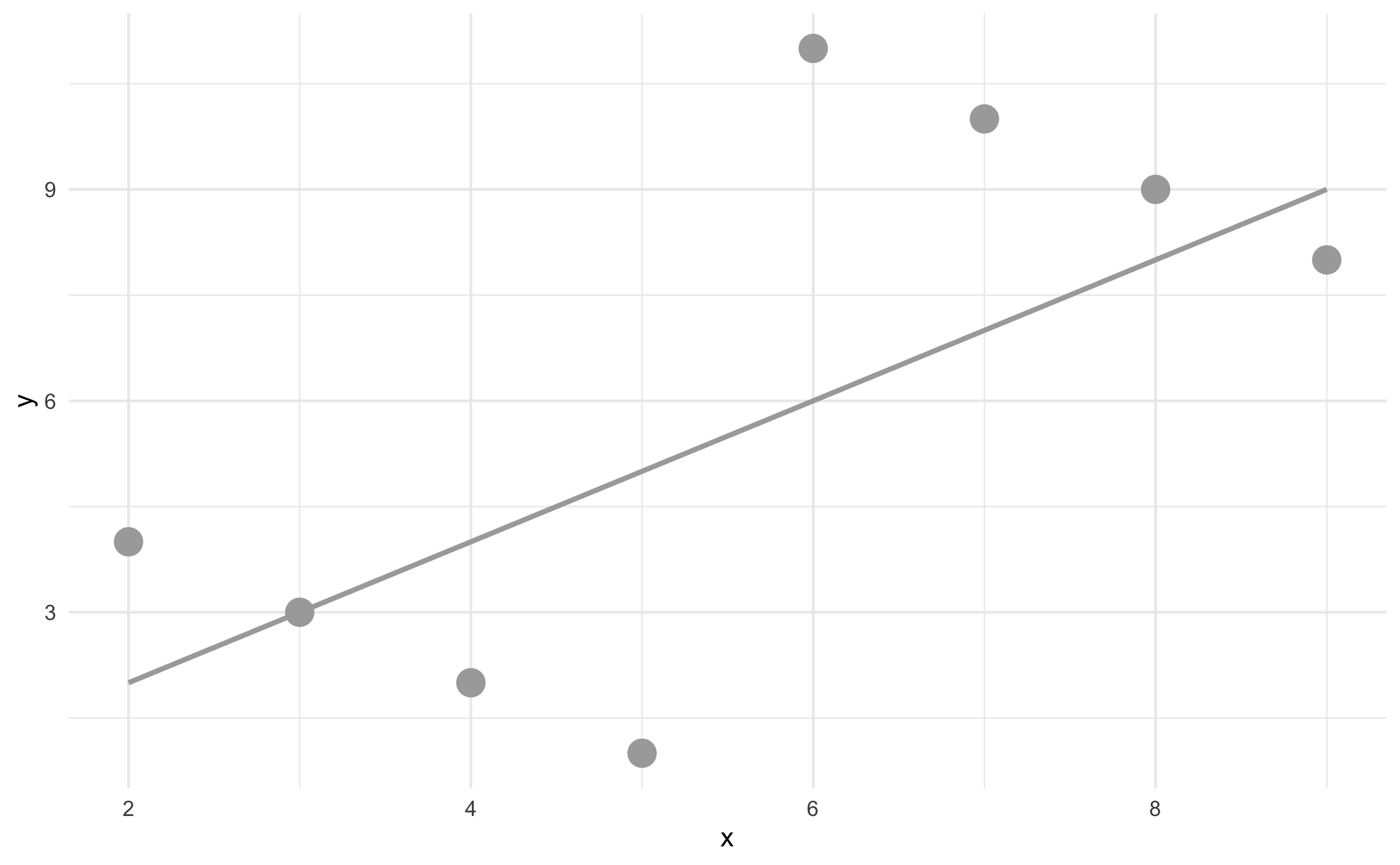
15 / 26
Considering a third variable
## # A tibble: 8 × 3## x y z ## <dbl> <dbl> <chr>## 1 2 4 A ## 2 3 3 A ## 3 4 2 A ## 4 5 1 A ## 5 6 11 B ## 6 7 10 B ## # … with 2 more rows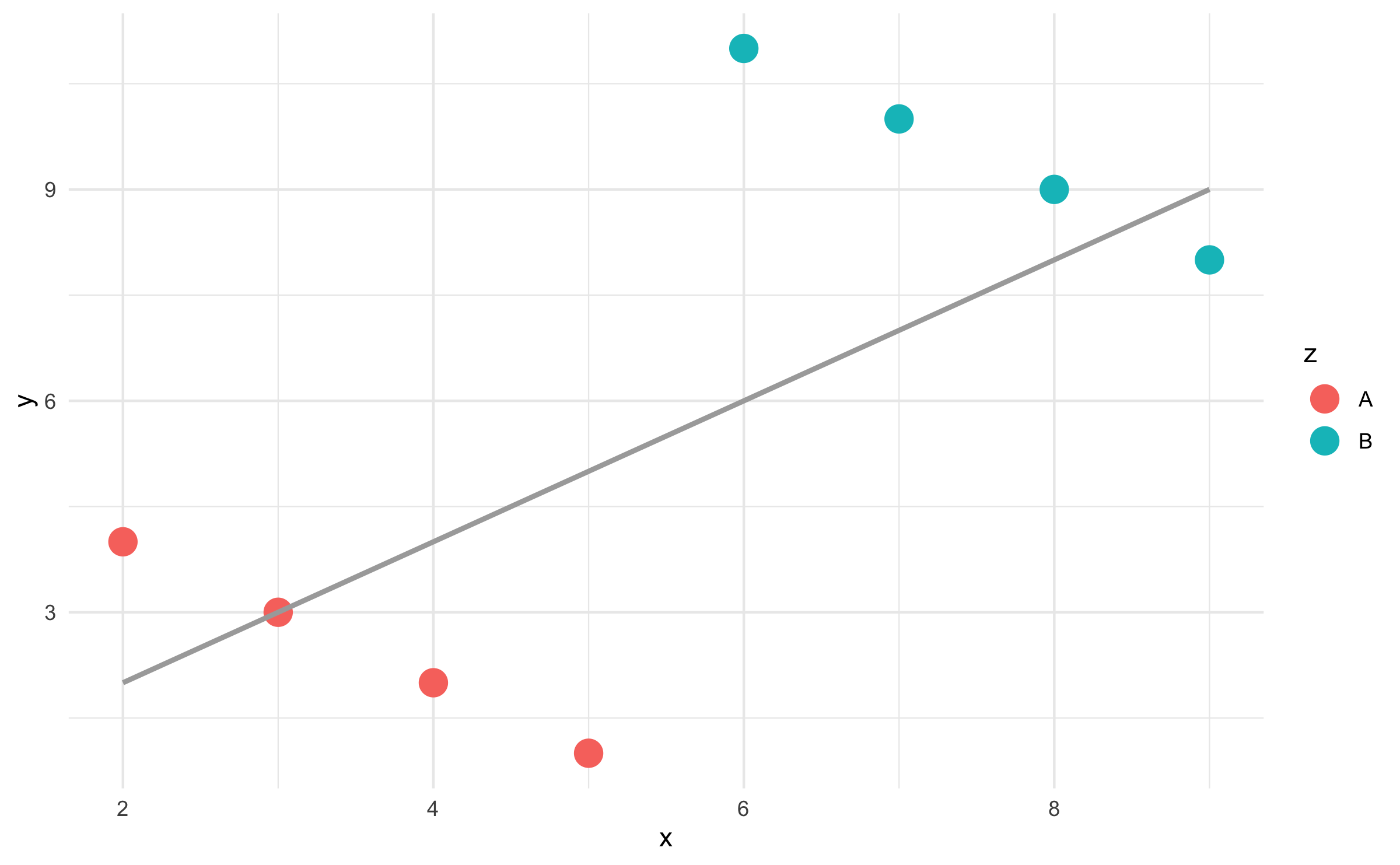
16 / 26
Relationship between three variables
## # A tibble: 8 × 3## x y z ## <dbl> <dbl> <chr>## 1 2 4 A ## 2 3 3 A ## 3 4 2 A ## 4 5 1 A ## 5 6 11 B ## 6 7 10 B ## # … with 2 more rows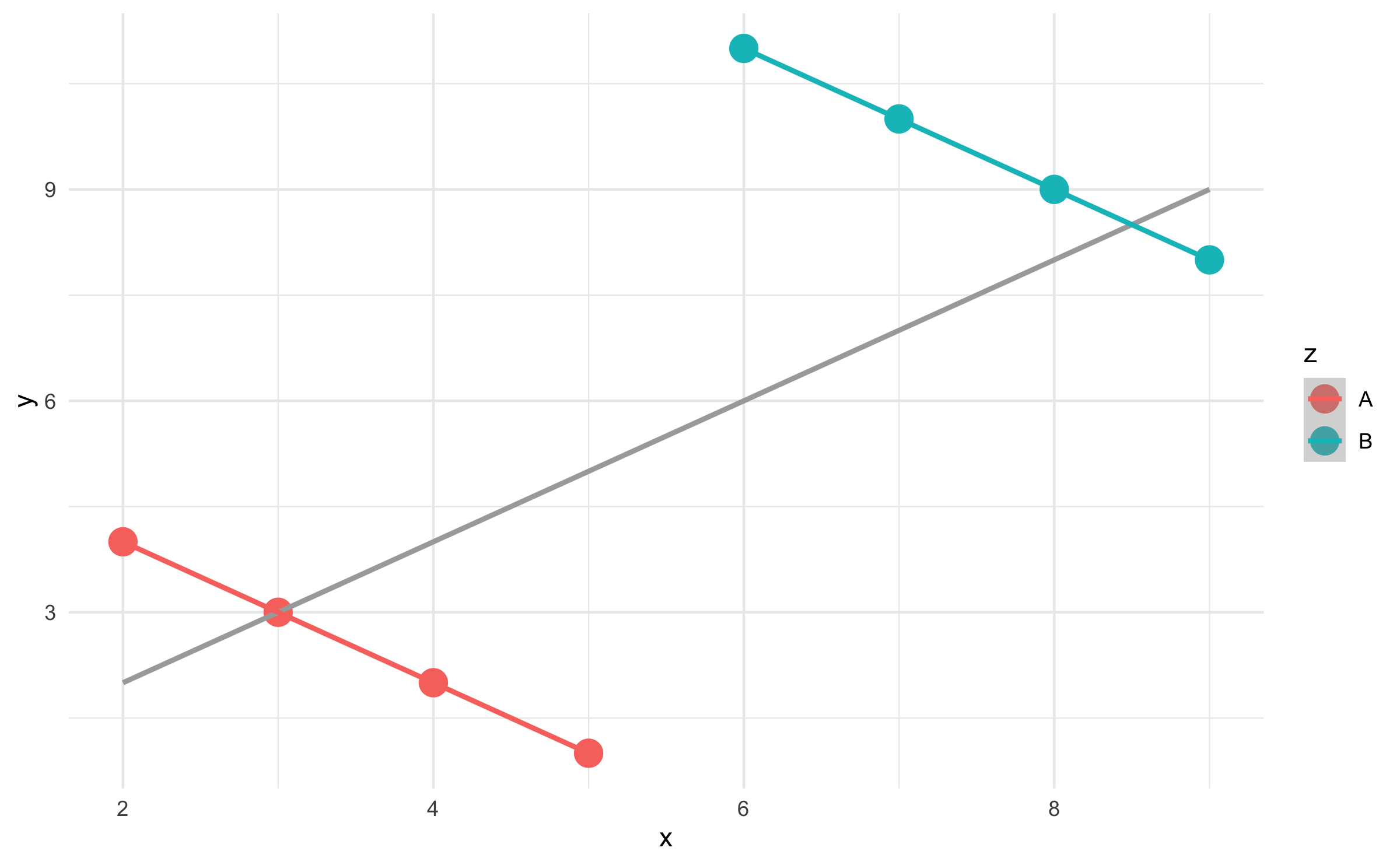
17 / 26
Simpson's paradox
- Not considering an important variable when studying a relationship can result in Simpson's paradox
- Simpson's paradox illustrates the effect that omission of an explanatory variable can have on the measure of association between another explanatory variable and a response variable
- The inclusion of a third variable in the analysis can change the apparent relationship between the other two variables
18 / 26
What does group_by() do?
group_by() takes an existing data frame and converts it into a grouped data frame where subsequent operations are performed "once per group"
ucbadmit## # A tibble: 4,526 × 3## admit gender dept ## <fct> <fct> <ord>## 1 Admitted Male A ## 2 Admitted Male A ## 3 Admitted Male A ## 4 Admitted Male A ## 5 Admitted Male A ## 6 Admitted Male A ## # … with 4,520 more rowsucbadmit %>% group_by(gender)## # A tibble: 4,526 × 3## # Groups: gender [2]## admit gender dept ## <fct> <fct> <ord>## 1 Admitted Male A ## 2 Admitted Male A ## 3 Admitted Male A ## 4 Admitted Male A ## 5 Admitted Male A ## 6 Admitted Male A ## # … with 4,520 more rows20 / 26
What does group_by() not do?
group_by() does not sort the data, arrange() does
ucbadmit %>% group_by(gender)## # A tibble: 4,526 × 3## # Groups: gender [2]## admit gender dept ## <fct> <fct> <ord>## 1 Admitted Male A ## 2 Admitted Male A ## 3 Admitted Male A ## 4 Admitted Male A ## 5 Admitted Male A ## 6 Admitted Male A ## # … with 4,520 more rowsucbadmit %>% arrange(gender)## # A tibble: 4,526 × 3## admit gender dept ## <fct> <fct> <ord>## 1 Admitted Female A ## 2 Admitted Female A ## 3 Admitted Female A ## 4 Admitted Female A ## 5 Admitted Female A ## 6 Admitted Female A ## # … with 4,520 more rows21 / 26
What does group_by() not do?
group_by() does not create frequency tables, count() does
ucbadmit %>% group_by(gender)## # A tibble: 4,526 × 3## # Groups: gender [2]## admit gender dept ## <fct> <fct> <ord>## 1 Admitted Male A ## 2 Admitted Male A ## 3 Admitted Male A ## 4 Admitted Male A ## 5 Admitted Male A ## 6 Admitted Male A ## # … with 4,520 more rowsucbadmit %>% count(gender)## # A tibble: 2 × 2## gender n## <fct> <int>## 1 Female 1835## 2 Male 269122 / 26
Undo grouping with ungroup()
ucbadmit %>% count(gender, admit) %>% group_by(gender) %>% mutate(prop_admit = n / sum(n)) %>% select(gender, prop_admit)## # A tibble: 4 × 2## # Groups: gender [2]## gender prop_admit## <fct> <dbl>## 1 Female 0.696## 2 Female 0.304## 3 Male 0.555## 4 Male 0.445ucbadmit %>% count(gender, admit) %>% group_by(gender) %>% mutate(prop_admit = n / sum(n)) %>% select(gender, prop_admit) %>% ungroup()## # A tibble: 4 × 2## gender prop_admit## <fct> <dbl>## 1 Female 0.696## 2 Female 0.304## 3 Male 0.555## 4 Male 0.44523 / 26
count() is a short-hand
count() is a short-hand for group_by() and then summarise() to count the number of observations in each group
ucbadmit %>% group_by(gender) %>% summarise(n = n())## # A tibble: 2 × 2## gender n## <fct> <int>## 1 Female 1835## 2 Male 2691ucbadmit %>% count(gender)## # A tibble: 2 × 2## gender n## <fct> <int>## 1 Female 1835## 2 Male 269124 / 26
count can take multiple arguments
ucbadmit %>% group_by(gender, admit) %>% summarise(n = n())## # A tibble: 4 × 3## # Groups: gender [2]## gender admit n## <fct> <fct> <int>## 1 Female Rejected 1278## 2 Female Admitted 557## 3 Male Rejected 1493## 4 Male Admitted 1198ucbadmit %>% count(gender, admit)## # A tibble: 4 × 3## gender admit n## <fct> <fct> <int>## 1 Female Rejected 1278## 2 Female Admitted 557## 3 Male Rejected 1493## 4 Male Admitted 119825 / 26
summarise() after group_by()
count()ungroups after itselfsummarise()peels off one layer of grouping by default, or you can specify a different behaviour
ucbadmit %>% group_by(gender, admit) %>% summarise(n = n())## # A tibble: 4 × 3## # Groups: gender [2]## gender admit n## <fct> <fct> <int>## 1 Female Rejected 1278## 2 Female Admitted 557## 3 Male Rejected 1493## 4 Male Admitted 119826 / 26