class: center, middle, inverse, title-slide .title[ # Logistic regression ] .subtitle[ ## <br><br> Data Science in a Box ] .author[ ### <a href="https://datasciencebox.org/">datasciencebox.org</a> ] --- layout: true <div class="my-footer"> <span> <a href="https://datasciencebox.org" target="_blank">datasciencebox.org</a> </span> </div> --- class: middle # Predicting categorical data --- ## Spam filters .pull-left-narrow[ - Data from 3921 emails and 21 variables on them - Outcome: whether the email is spam or not - Predictors: number of characters, whether the email had "Re:" in the subject, time at which email was sent, number of times the word "inherit" shows up in the email, etc. ] .pull-right-wide[ .small[ ```r library(openintro) glimpse(email) ``` ``` ## Rows: 3,921 ## Columns: 21 ## $ spam <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ to_multiple <fct> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, … ## $ from <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, … ## $ cc <int> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, … ## $ sent_email <fct> 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, … ## $ time <dttm> 2012-01-01 01:16:41, 2012-01-01 02:03:59,… ## $ image <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, … ## $ attach <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, … ## $ dollar <dbl> 0, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ winner <fct> no, no, no, no, no, no, no, no, no, no, no… ## $ inherit <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ viagra <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ password <dbl> 0, 0, 0, 0, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ num_char <dbl> 11.370, 10.504, 7.773, 13.256, 1.231, 1.09… ## $ line_breaks <int> 202, 202, 192, 255, 29, 25, 193, 237, 69, … ## $ format <fct> 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, … ## $ re_subj <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, … ## $ exclaim_subj <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ urgent_subj <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, … ## $ exclaim_mess <dbl> 0, 1, 6, 48, 1, 1, 1, 18, 1, 0, 2, 1, 0, 1… ## $ number <fct> big, small, small, small, none, none, big,… ``` ] ] --- .question[ Would you expect longer or shorter emails to be spam? 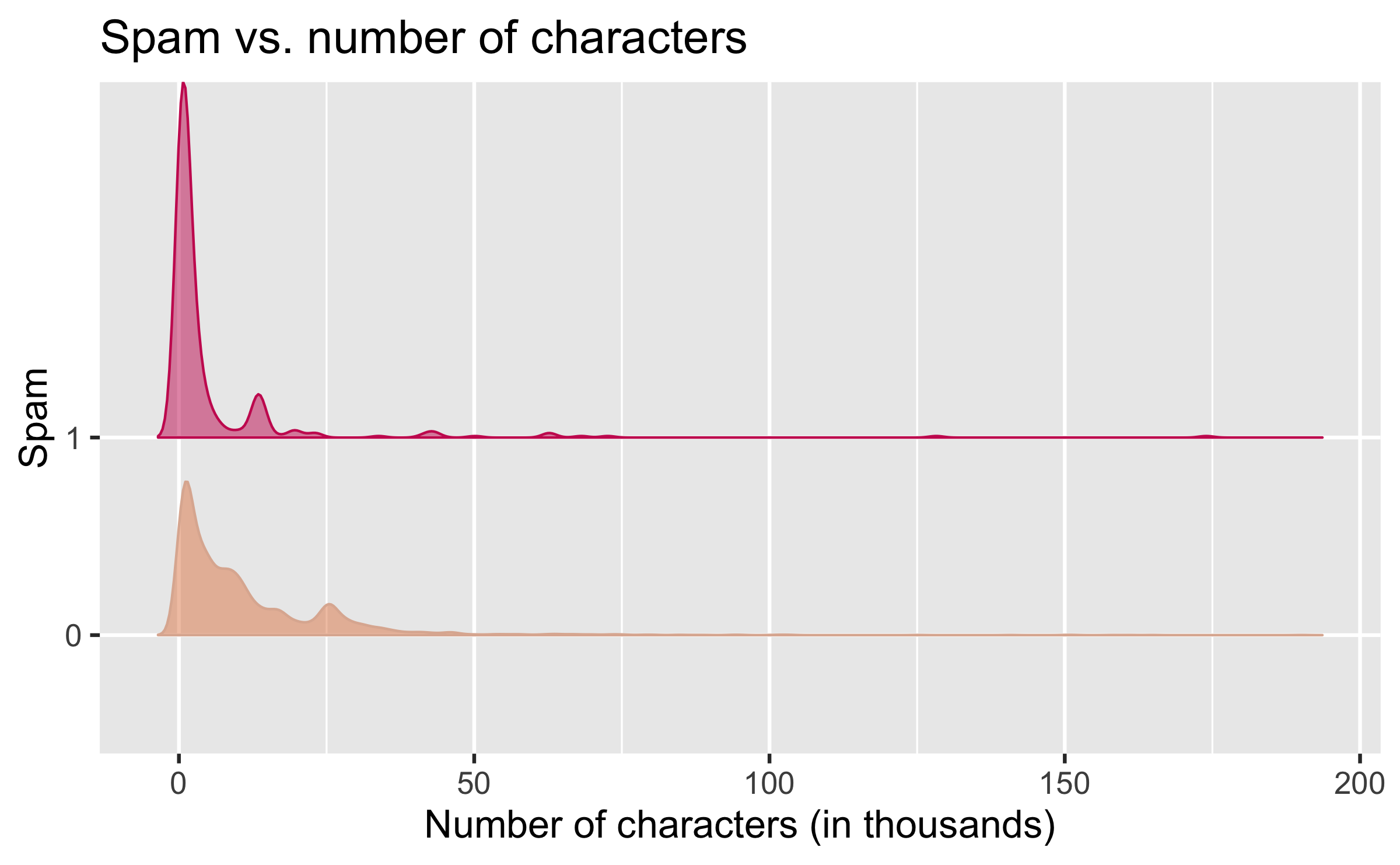] -- .pull-left[ <img src="u4-d06-logistic-reg_files/figure-html/unnamed-chunk-3-1.png" width="100%" style="display: block; margin: auto;" /> ] .pull-right[ ``` ## # A tibble: 2 × 2 ## spam mean_num_char ## <fct> <dbl> ## 1 0 11.3 ## 2 1 5.44 ``` ] --- .question[ Would you expect emails that have subjects starting with "Re:", "RE:", "re:", or "rE:" to be spam or not? ] -- <img src="u4-d06-logistic-reg_files/figure-html/unnamed-chunk-5-1.png" width="60%" style="display: block; margin: auto;" /> --- ## Modelling spam - Both number of characters and whether the message has "re:" in the subject might be related to whether the email is spam. How do we come up with a model that will let us explore this relationship? -- - For simplicity, we'll focus on the number of characters (`num_char`) as predictor, but the model we describe can be expanded to take multiple predictors as well. --- ## Modelling spam This isn't something we can reasonably fit a linear model to -- we need something different! <img src="u4-d06-logistic-reg_files/figure-html/unnamed-chunk-6-1.png" width="70%" style="display: block; margin: auto;" /> --- ## Framing the problem - We can treat each outcome (spam and not) as successes and failures arising from separate Bernoulli trials - Bernoulli trial: a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted -- - Each Bernoulli trial can have a separate probability of success $$ y_i ∼ Bern(p) $$ -- - We can then use the predictor variables to model that probability of success, `\(p_i\)` -- - We can't just use a linear model for `\(p_i\)` (since `\(p_i\)` must be between 0 and 1) but we can transform the linear model to have the appropriate range --- ## Generalized linear models - This is a very general way of addressing many problems in regression and the resulting models are called **generalized linear models (GLMs)** -- - Logistic regression is just one example --- ## Three characteristics of GLMs All GLMs have the following three characteristics: 1. A probability distribution describing a generative model for the outcome variable -- 2. A linear model: `$$\eta = \beta_0 + \beta_1 X_1 + \cdots + \beta_k X_k$$` -- 3. A link function that relates the linear model to the parameter of the outcome distribution --- class: middle # Logistic regression --- ## Logistic regression - Logistic regression is a GLM used to model a binary categorical outcome using numerical and categorical predictors -- - To finish specifying the Logistic model we just need to define a reasonable link function that connects `\(\eta_i\)` to `\(p_i\)`: logit function -- - **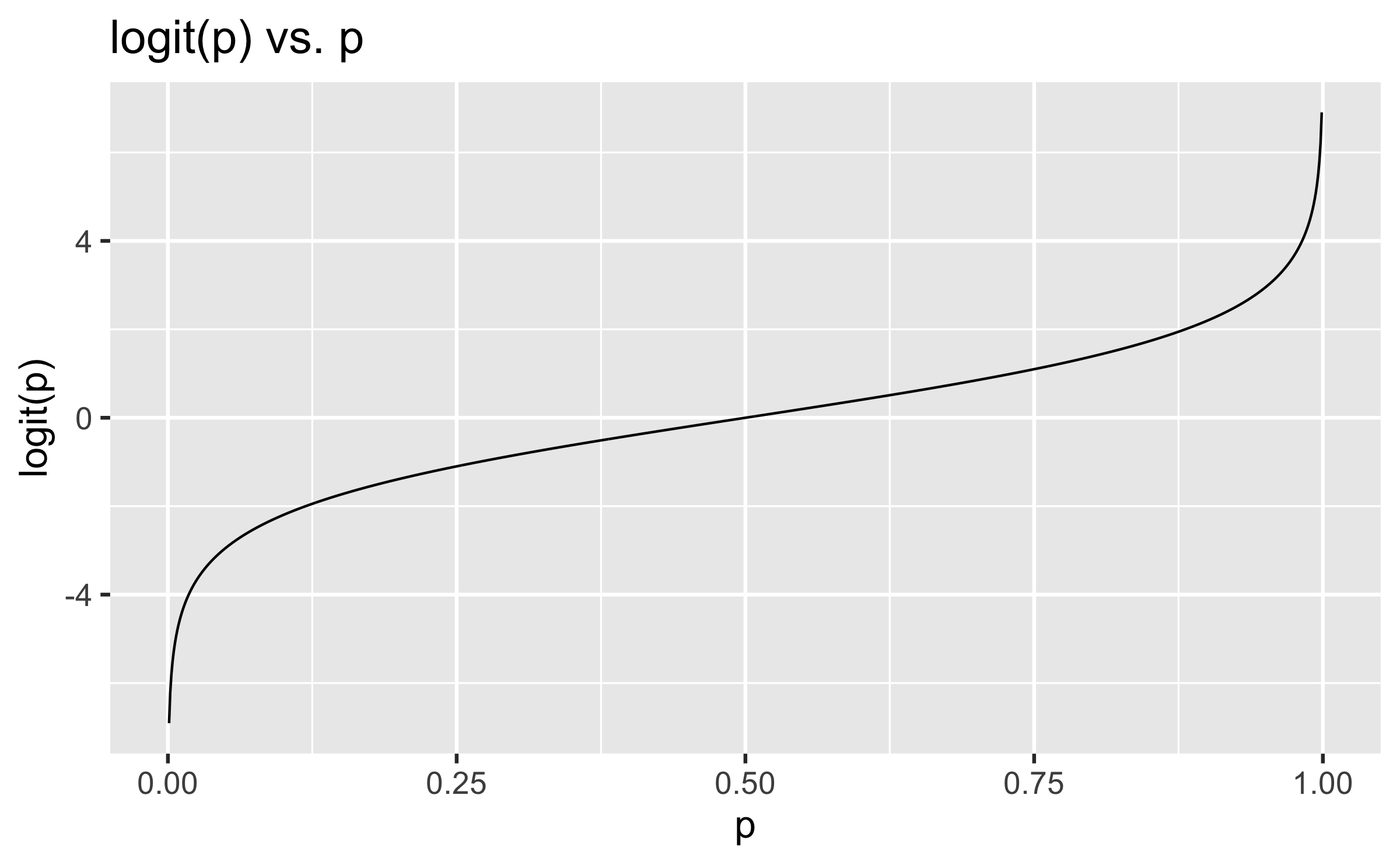Logit function:** For `\(0\le p \le 1\)` `$$logit(p) = \log\left(\frac{p}{1-p}\right)$$` --- ## Logit function, visualised <img src="u4-d06-logistic-reg_files/figure-html/unnamed-chunk-7-1.png" width="60%" style="display: block; margin: auto;" /> --- ## Properties of the logit - The logit function takes a value between 0 and 1 and maps it to a value between `\(-\infty\)` and `\(\infty\)` -- - Inverse logit (logistic) function: `$$g^{-1}(x) = \frac{\exp(x)}{1+\exp(x)} = \frac{1}{1+\exp(-x)}$$` -- - The inverse logit function takes a value between `\(-\infty\)` and `\(\infty\)` and maps it to a value between 0 and 1 -- - This formulation is also useful for interpreting the model, since the logit can be interpreted as the log odds of a success -- more on this later --- ## The logistic regression model - Based on the three GLM criteria we have - `\(y_i \sim \text{Bern}(p_i)\)` - `\(\eta_i = \beta_0+\beta_1 x_{1,i} + \cdots + \beta_n x_{n,i}\)` - `\(\text{logit}(p_i) = \eta_i\)` -- - From which we get `$$p_i = \frac{\exp(\beta_0+\beta_1 x_{1,i} + \cdots + \beta_k x_{k,i})}{1+\exp(\beta_0+\beta_1 x_{1,i} + \cdots + \beta_k x_{k,i})}$$` --- ## Modeling spam In R we fit a GLM in the same way as a linear model except we - specify the model with `logistic_reg()` - use `"glm"` instead of `"lm"` as the engine - define `family = "binomial"` for the link function to be used in the model -- ```r spam_fit <- logistic_reg() %>% set_engine("glm") %>% fit(spam ~ num_char, data = email, family = "binomial") tidy(spam_fit) ``` ``` ## # A tibble: 2 × 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) -1.80 0.0716 -25.1 2.04e-139 ## 2 num_char -0.0621 0.00801 -7.75 9.50e- 15 ``` --- ## Spam model ```r tidy(spam_fit) ``` ``` ## # A tibble: 2 × 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) -1.80 0.0716 -25.1 2.04e-139 ## 2 num_char -0.0621 0.00801 -7.75 9.50e- 15 ``` -- Model: `$$\log\left(\frac{p}{1-p}\right) = -1.80-0.0621\times \text{num_char}$$` --- ## 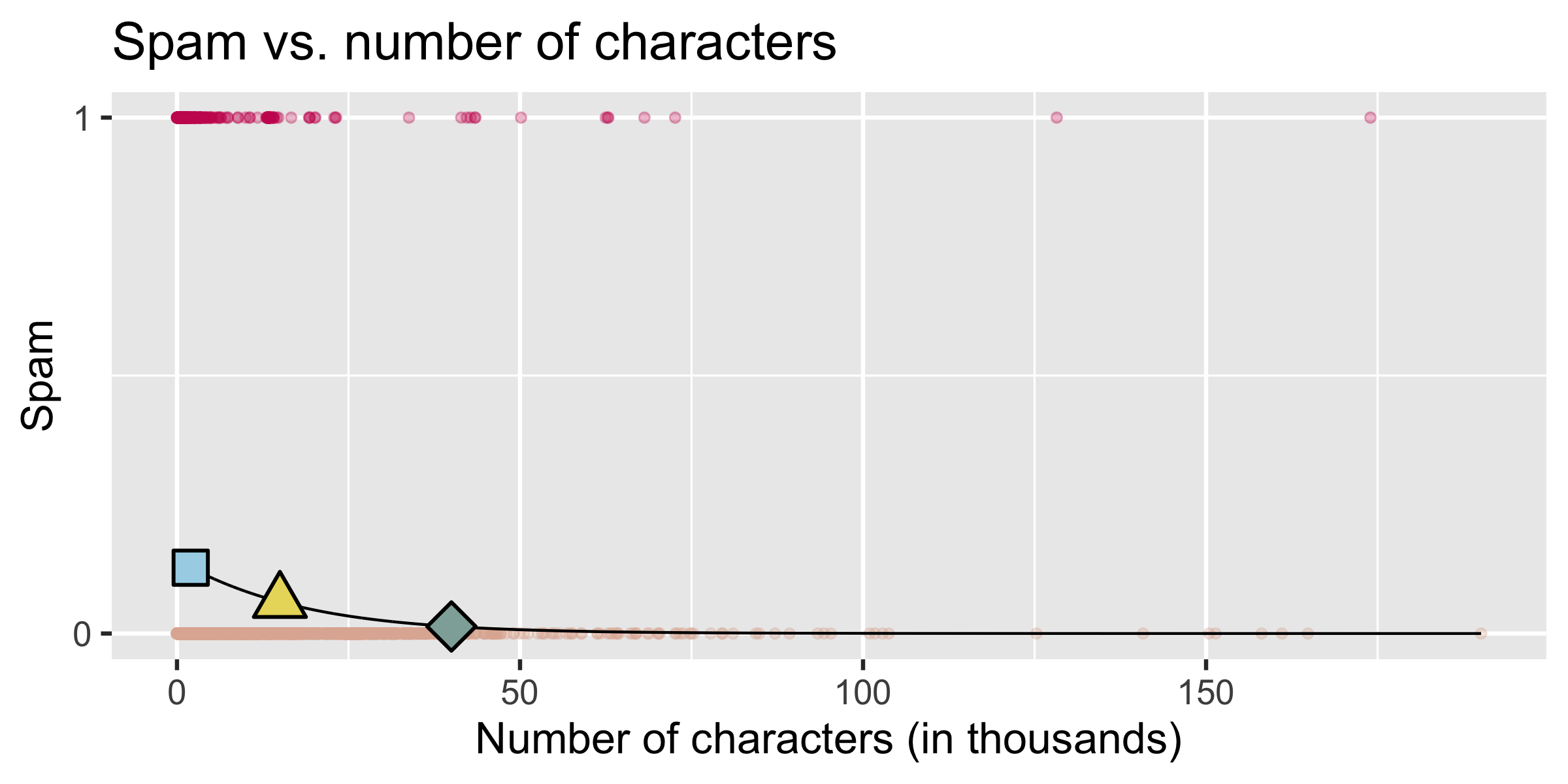P(spam) for an email with 2000 characters `$$\log\left(\frac{p}{1-p}\right) = -1.80-0.0621\times 2$$` -- `$$\frac{p}{1-p} = \exp(-1.9242) = 0.15 \rightarrow p = 0.15 \times (1 - p)$$` -- `$$p = 0.15 - 0.15p \rightarrow 1.15p = 0.15$$` -- `$$p = 0.15 / 1.15 = 0.13$$` --- .question[ What is the probability that an email with 15000 characters is spam? What about an email with 40000 characters? 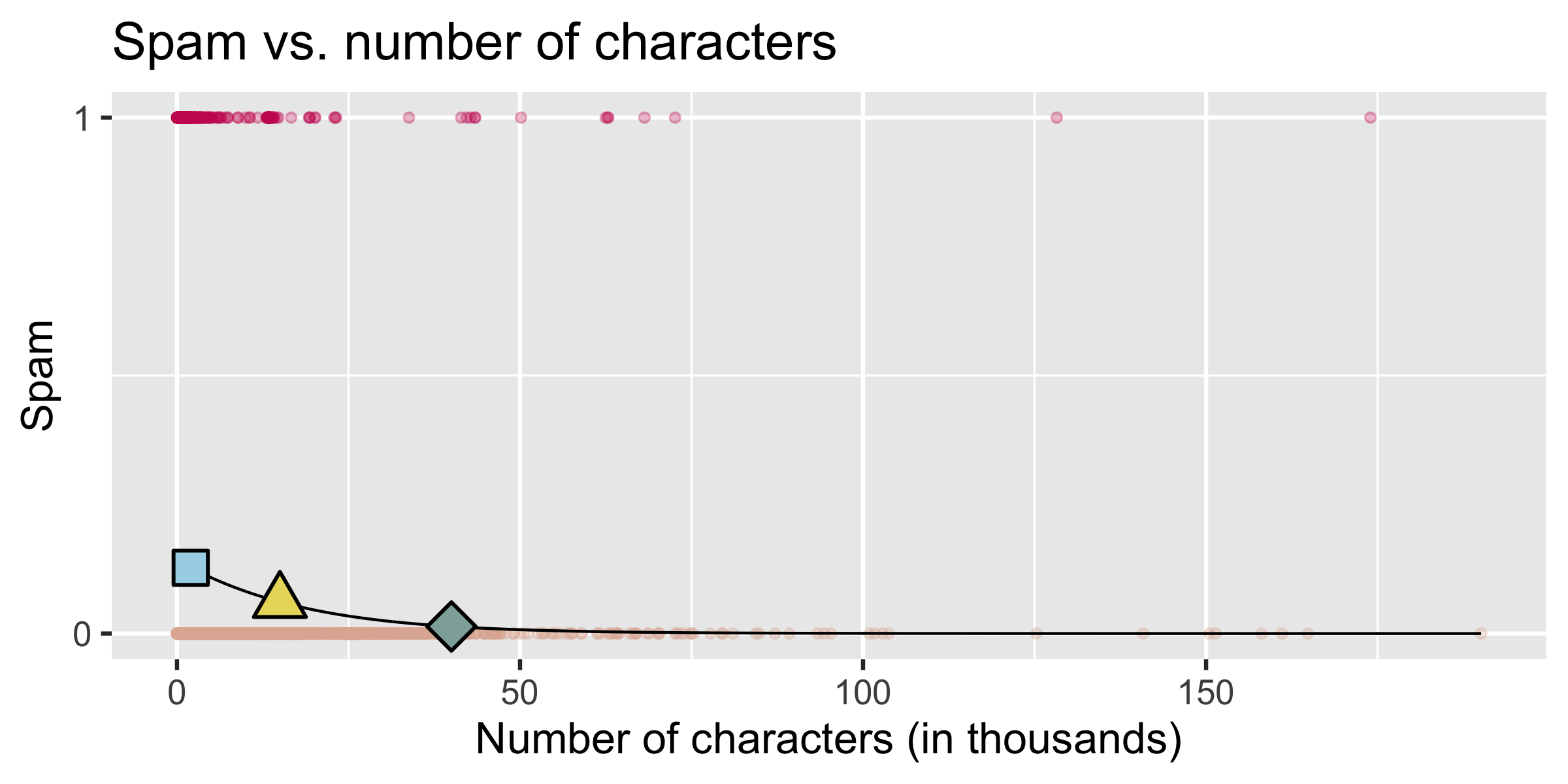] -- .pull-left[ <img src="u4-d06-logistic-reg_files/figure-html/spam-predict-viz-1.png" width="100%" style="display: block; margin: auto;" /> ] .pull-right[ - .light-blue[2K chars: P(spam) = 0.13] - .yellow[15K chars, P(spam) = 0.06] - .green[40K chars, P(spam) = 0.01] ] --- .question[ Would you prefer an email with 2000 characters to be labelled as spam or not? How about 40,000 characters? ] <img src="u4-d06-logistic-reg_files/figure-html/unnamed-chunk-10-1.png" width="60%" style="display: block; margin: auto;" /> --- class: middle # Sensitivity and specificity --- ## False positive and negative | | Email is spam | Email is not spam | |-------------------------|-------------------------------|-------------------------------| | Email labelled spam | True positive | False positive (Type 1 error) | | Email labelled not spam | False negative (Type 2 error) | True negative | -- - False negative rate = P(Labelled not spam | Email spam) = FN / (TP + FN) - False positive rate = P(Labelled spam | Email not spam) = FP / (FP + TN) --- ## Sensitivity and specificity | | Email is spam | Email is not spam | |-------------------------|-------------------------------|-------------------------------| | Email labelled spam | True positive | False positive (Type 1 error) | | Email labelled not spam | False negative (Type 2 error) | True negative | -- - Sensitivity = P(Labelled spam | Email spam) = TP / (TP + FN) - Sensitivity = 1 − False negative rate - Specificity = P(Labelled not spam | Email not spam) = TN / (FP + TN) - Specificity = 1 − False positive rate --- .question[ If you were designing a spam filter, would you want sensitivity and specificity to be high or low? What are the trade-offs associated with each decision? ]