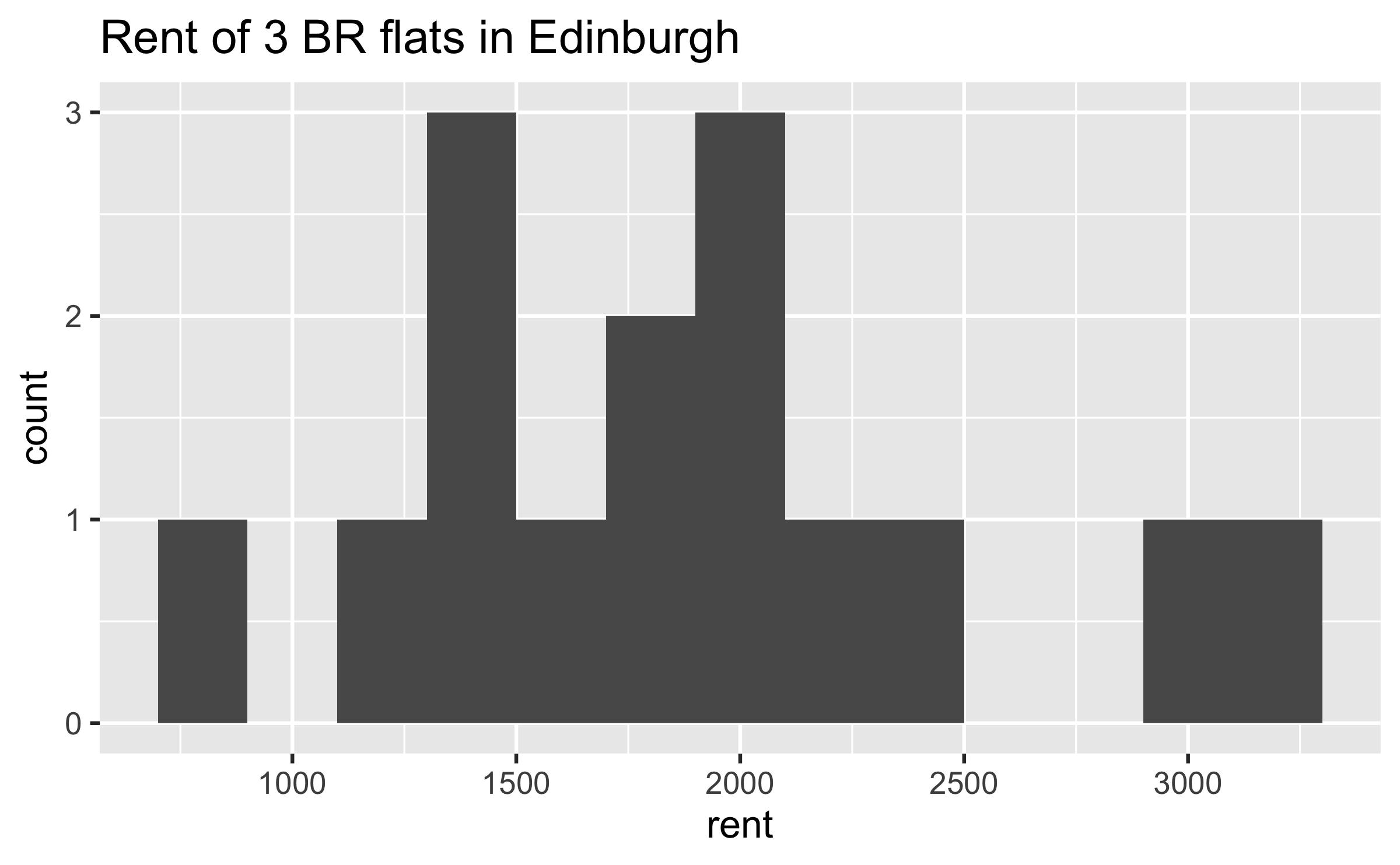
Rent in Edinburgh
Take a guess! How much does a typical 3 BR flat in Edinburgh rents for?
Sample
Fifteen 3 BR flats in Edinburgh were randomly selected on rightmove.co.uk.
library(tidyverse)edi_3br <- read_csv2("data/edi-3br.csv") # ; separated## # A tibble: 15 × 4## flat_id rent title address ## <chr> <dbl> <chr> <chr> ## 1 flat_01 825 3 bedroom apartment to rent Burnhead Grove, Edin…## 2 flat_02 2400 3 bedroom flat to rent Simpson Loan, Quarte…## 3 flat_03 1900 3 bedroom flat to rent FETTES ROW, NEW TOWN…## 4 flat_04 1500 3 bedroom apartment to rent Eyre Crescent, Edinb…## 5 flat_05 3250 3 bedroom flat to rent Walker Street, Edinb…## 6 flat_06 2145 3 bedroom flat to rent George Street, City …## # … with 9 more rowsBootstrap population
Generated assuming there are more flats like the ones in the observed sample... Population mean = ❓

Bootstrapping scheme
- Take a bootstrap sample - a random sample taken with replacement from the original sample, of the same size as the original sample
- Calculate the bootstrap statistic - a statistic such as mean, median, proportion, slope, etc. computed on the bootstrap samples
- Repeat steps (1) and (2) many times to create a bootstrap distribution - a distribution of bootstrap statistics
- Calculate the bounds of the XX% confidence interval as the middle XX% of the bootstrap distribution
Generate bootstrap means
edi_3br %>% # specify the variable of interest specify(response = rent)Generate bootstrap means
edi_3br %>% # specify the variable of interest specify(response = rent) # generate 15000 bootstrap samples generate(reps = 15000, type = "bootstrap")Generate bootstrap means
edi_3br %>% # specify the variable of interest specify(response = rent) # generate 15000 bootstrap samples generate(reps = 15000, type = "bootstrap") # calculate the mean of each bootstrap sample calculate(stat = "mean")Generate bootstrap means
# save resulting bootstrap distributionboot_df <- edi_3br %>% # specify the variable of interest specify(response = rent) %>% # generate 15000 bootstrap samples generate(reps = 15000, type = "bootstrap") %>% # calculate the mean of each bootstrap sample calculate(stat = "mean")The bootstrap sample
How many observations are there in boot_df? What does each observation represent?
boot_df## Response: rent (numeric)## # A tibble: 15,000 × 2## replicate stat## <int> <dbl>## 1 1 1793.## 2 2 1938.## 3 3 2175 ## 4 4 2159.## 5 5 2084 ## 6 6 1761 ## # … with 14,994 more rowsVisualize the bootstrap distribution
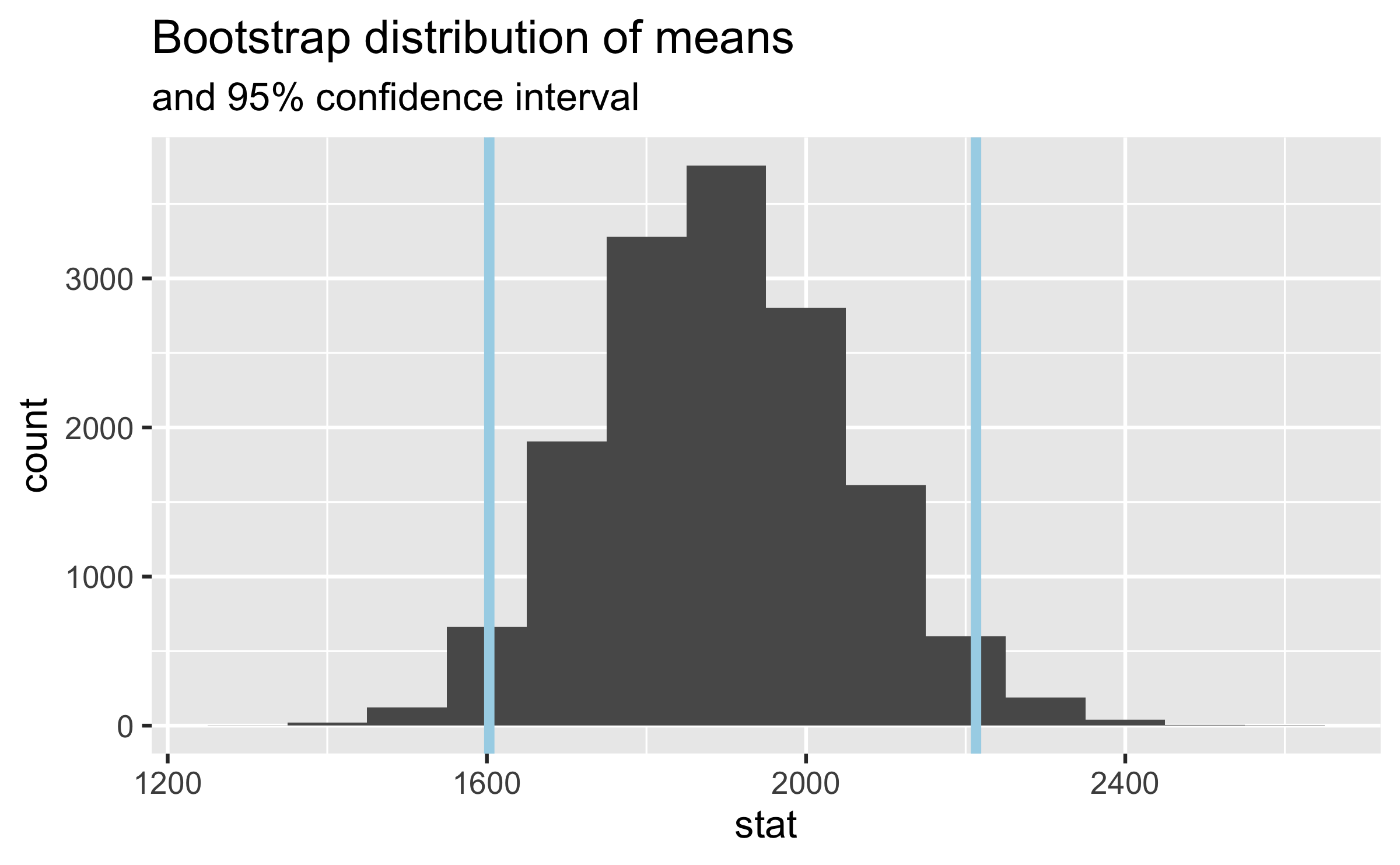
ggplot(data = boot_df, mapping = aes(x = stat)) + geom_histogram(binwidth = 100) + labs(title = "Bootstrap distribution of means")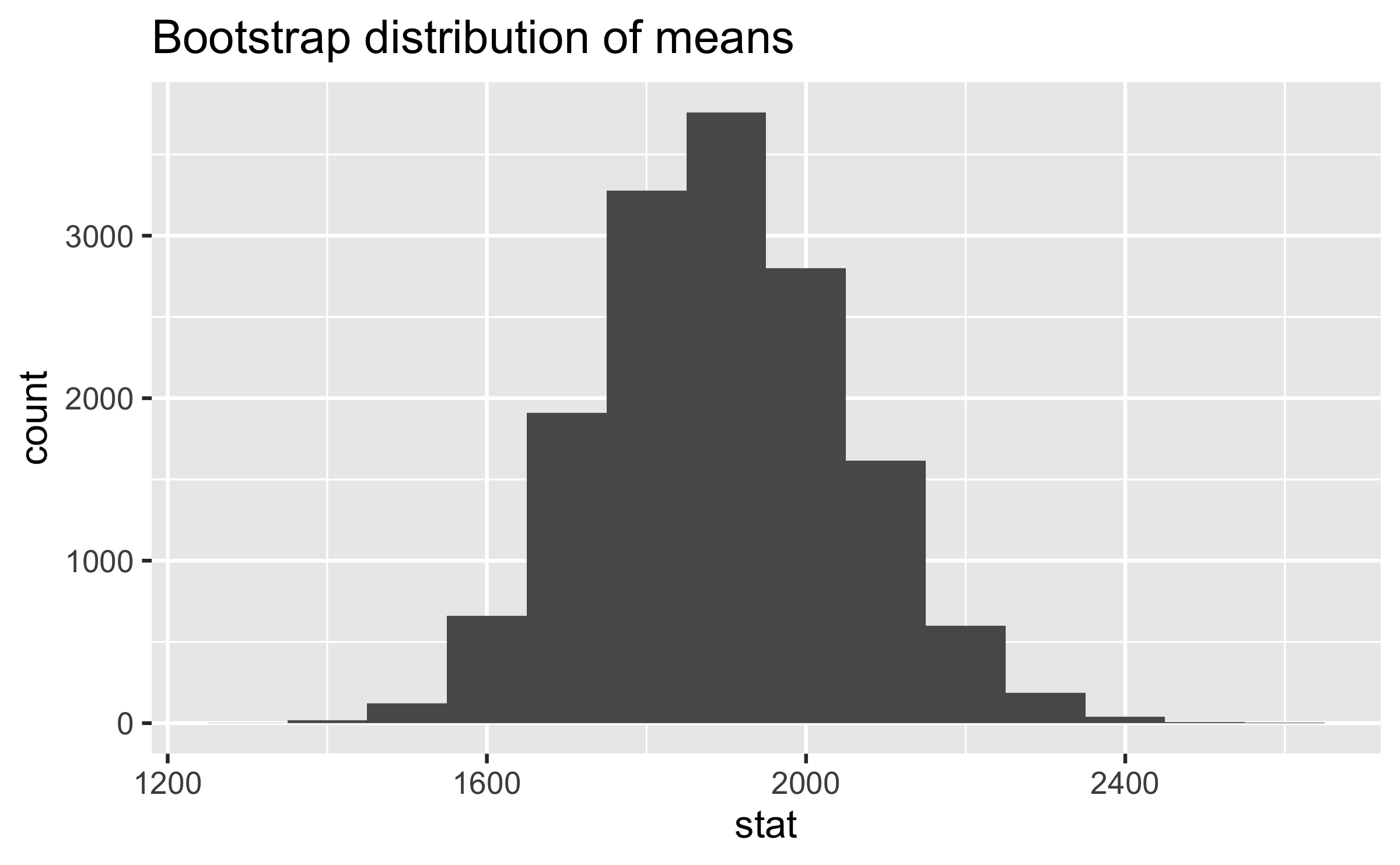
Calculate the confidence interval
A 95% confidence interval is bounded by the middle 95% of the bootstrap distribution.
boot_df %>% summarize(lower = quantile(stat, 0.025), upper = quantile(stat, 0.975))## # A tibble: 1 × 2## lower upper## <dbl> <dbl>## 1 1603. 2213.Interpret the confidence interval
The 95% confidence interval for the mean rent of three bedroom flats in Edinburgh was calculated as (1603, 2213). Which of the following is the correct interpretation of this interval?
(a) 95% of the time the mean rent of three bedroom flats in this sample is between £1603 and £2213.
(b) 95% of all three bedroom flats in Edinburgh have rents between £1603 and £2213.
(c) We are 95% confident that the mean rent of all three bedroom flats is between £1603 and £2213.
(d) We are 95% confident that the mean rent of three bedroom flats in this sample is between £1603 and £2213.
Confidence level
We are 95% confident that ...
- Suppose we took many samples from the original population and built a 95% confidence interval based on each sample.
- Then about 95% of those intervals would contain the true population parameter.
Commonly used confidence levels
Which line (orange dash/dot, blue dash, green dot) represents which confidence level?
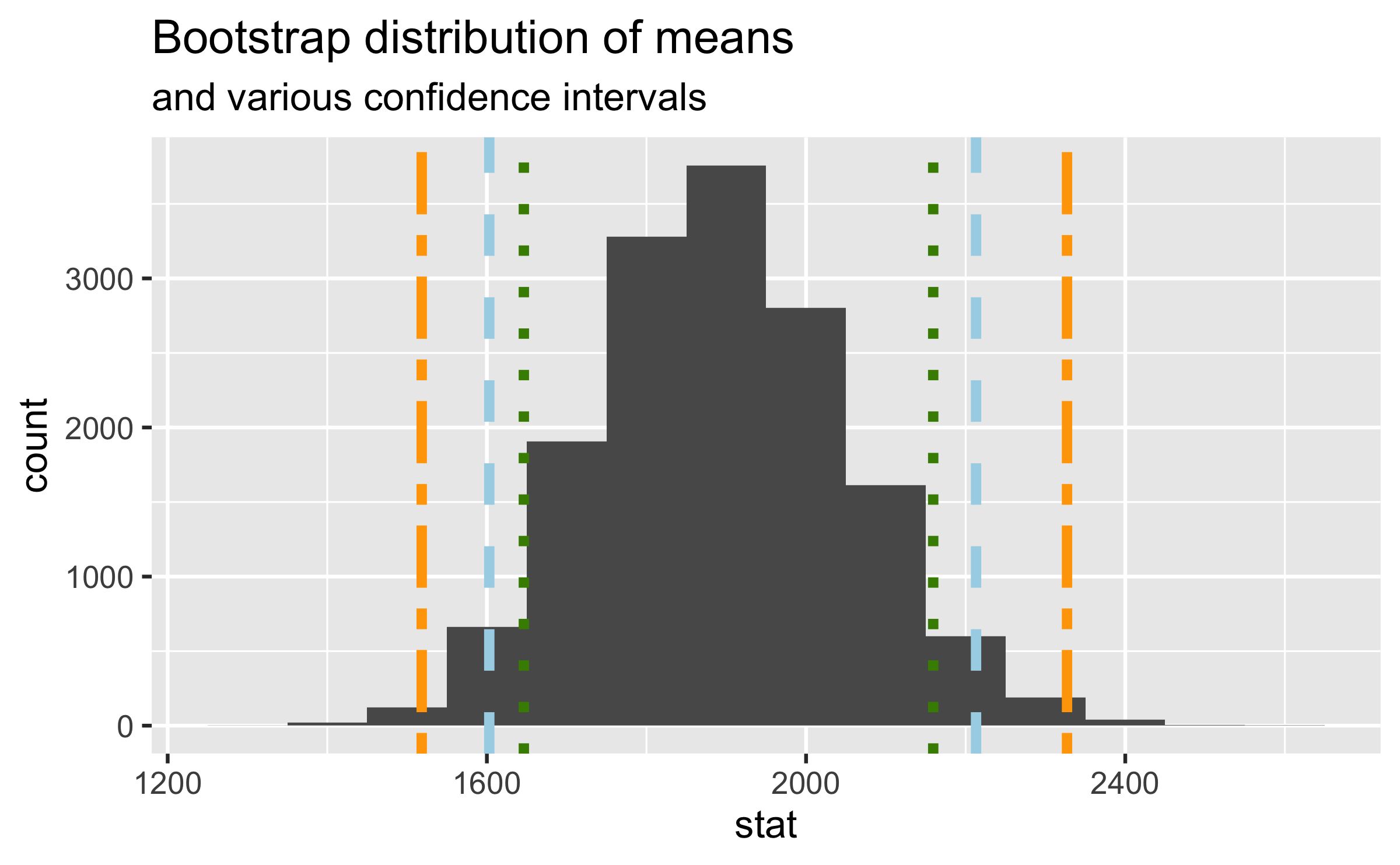
Precision vs. accuracy
If we want to be very certain that we capture the population parameter, should we use a wider or a narrower interval? What drawbacks are associated with using a wider interval?
Precision vs. accuracy
If we want to be very certain that we capture the population parameter, should we use a wider or a narrower interval? What drawbacks are associated with using a wider interval?

Precision vs. accuracy
If we want to be very certain that we capture the population parameter, should we use a wider or a narrower interval? What drawbacks are associated with using a wider interval?

How can we get best of both worlds -- high precision and high accuracy?
Changing confidence level
How would you modify the following code to calculate a 90% confidence interval? How would you modify it for a 99% confidence interval?
edi_3br %>% specify(response = rent) %>% generate(reps = 15000, type = "bootstrap") %>% calculate(stat = "mean") %>% summarize(lower = quantile(stat, 0.025), upper = quantile(stat, 0.975))Recap
- Sample statistic ≠ population parameter, but if the sample is good, it can be a good estimate
- We report the estimate with a confidence interval, and the width of this interval depends on the variability of sample statistics from different samples from the population
- Since we can't continue sampling from the population, we bootstrap from the one sample we have to estimate sampling variability
- We can do this for any sample statistic:
- For a mean:
calculate(stat = "mean") - For a median:
calculate(stat = "median") - Learn about calculating bootstrap intervals for other statistics in your homework
- For a mean: